MIT Linear Algebra Study Lec 14 - 19
________________________________________________________________________________________________
MIT Gilbert Strang : Lecture 14 ( Orthogonal Vectors and Subspaces )
Orthogonal vectors & Subspaces
nullspace ⊥ row space
N(A^T * A) = N(A)
* The angle between the two sub-spaces is 90 degrees (Orthogonal)
Orthogonal vectors
Pythagoras figured out that vectors x and y are orthogonal when x^T * y = 0
* So, 2 x^T * y = 0, when they are orthogonal
** Subspace S is orthogonal to subspace T
means : every vector in S is orthogonal to every vector in T
* for the case of orthogonal, they don't intersect in any non-zero vector.
row space is orthogonal to nullspace.
why? Ax = 0, so dot products of (row of A) · x = 0
which means the null space of x is orthogonal to every row.
null space and row space are orthogonal complements in R^n
Null space contains all vectors ⊥ row space.
Comming : Ax = b when there is no solution.
" Solve " m > n
* when A is n x m matrix ( m > n )
(A^T) A is square, symetric, n x n
Ax = b -> (A^T) A x = (A^T) b
* N(A^T A) = N(A)
* rank of A^T A = rank of A
* A^T A is invertible exactly if A has independent columns.
| An invertible matrix is nonsingular matrix (has solution) But not invertible is a singular matrix (has no solution) |
Ref) invertible matrix :
https://deep-learning-study.tistory.com/307
________________________________________________________________________________________________
MIT Gilbert Strang : Lecture 15 ( Projections onto Subspaces )
Projections
Least squares
Projection matrix
* when projecting b on a, the projected position is p and the error is e = b - p
* a^T (b - xa) = 0 --> a is perpendicular to (b - xa)
= x a^T * a = a^T * b
= "x = ( a^T * b ) / ( a^T * a )"
p = ax
p = a * (a^T * b) / (a^T * a)
* proj p = P b
* projection matrix P = (a * a^T) / (a^T * a)
+ parentheses -> (), {}, []
* C(P) = line through a , and the rank(P) = 1
* P^T = P it is symetric
* what if project the matrix b twice? it's the same
cause P * P = (a * a^T)(a * a^T) / (a^T * a)(a^T * a) = (a * a^T) / (a^T * a) = P
so the result p = Pb = P*Pb
** P^T = P , P * P = P
(1, 1), (2, 2), (3, 3)
** if the error e is massive then it's an outlier and we don't have to calculate those.
* and the errors are e1 = -1/6, e2 = +2/6, e3 = -1/6
* (Q Q^T)(Q Q^T) = Q Q^T
* Why project?
* Because Ax = b may have no solution, so to solve the closest problem that can be solved.
* Solve Ax^ = p (projection of b onto column space)
** So, it's like this when we have vector b that is not in the plane but can't be solved, so we should project b into the column space plane and which is p(nearest point), and solve the problem.
** how can we know the plane? by basis, like a1 and a2
they don't have to be perpendicular but they better be independent.
so It's a plane of a1 and a2 = column space of A = [ a1 a2 ]
** and error e = b - p (closest point) is perpendicular to the plane.
** what is projection P ? P = x1^ * a1 + x2^ * p2 = A x^
* P = A x^ and find x^
* key = b - Ax^ is perpendicular to the plane.
* so (b - Ax^) is perpendicular to every vector in that plane, so it's also perpendicular to each a1 and a2,
which is like a1^T (b -Ax^) = 0 , a2^T (b - Ax^) = 0
and this can be also shown like this,
which means A^T (b - Ax^) = 0
** And in this case e = (b - Ax^) and sub-spaces of e is in the N(A^T)
cause it's A^T * e = 0
*** so e ⊥ C(A)
* x^ = ((A^T A)^-1) * A^Tb
* p = A x^ = A*((A^T* A)^-1) * A^Tb =
projection matrix P = A * ((A^T * A)^ -1) * A^T
@ this is an additional test, if A was a square matrix the result will be the Identity matrix,
But A is not a square matrix so it can't have an inverse (A^T A is a square matrix so it can)
so we should leave the projection matrix just as it was.
 |
| wrong case |
but if the A is a square matrix and invertible,
then its column space is the whole R^n in n x n matrix.
it's projected onto the whole space so it's an Identity matrix.
* P^T = P , P*P = P
Least squares fitting by a line
fit the best points based on the line
** Can't solve Ax = b, but can solve (A^T)*A = (A^T)*b
________________________________________________________________________________________________
MIT Gilbert Strang : Lecture 16 ( Projection Matrices and Least Squares )
Projections
Least squares and
best straight line
Projection matrix
* P = A((A^T * A)^-1) A^T
* If b in column space Pb = b
* If b ⊥ column space Pb = 0 (dot product should be 0)
** If b is in column space then, Pb = A((A^T * A)^-1) A^T Ax
= A * ((A^T * A)^-1) * (A^T * A) * x
= Ax = b
** When we have vector b as a result, p is projected to position onto the column space, and e is projected onto the N(A^T) which is an error.
** so p + e = b
** p = Pb , e = (i - p)*b
Let's find the best straight line y = C + Dt
**
C + D = 1
C + 2D =2
C + 3D = 2
Ax = b
minimize ||Ax -b||^2 = ||e||^2
= e1^2 + e2^2 + e3^3
* given values are b1, b2, b3 and projected points are p1, p2, p3, and the distances between them are e1, e2, e3
p1, p2, p3 is in the column space, and we can solve the problem.
Find x^ , p
** A^T * A * x^ = A^T * b normal equations
** A^T * A should be symmetric and invertible
* Best line is (2/3) + (1/2) * t ( y= (2/3) + (1/2)t )
* So based on the best line p1 = 7/6, p2 = 5/3, p3 = 13/6
** b = p + e
* p and e, they are perpendicular. (dot prod of two vectors is 0)
* and e is also perpendicular to the column space
 |
| Column space |
 |
| p on the column space e on the N(A^T) |
* A^T A x^ = A^T b
* p = A x^
** If A has independent columns then A^T A is invertible.
suppose A^T Ax = 0 to prove x must be 0
Idea x^T * A^T * A x = 0 = (Ax)^T * (Ax) => this is the length of Ax squared so Ax = 0
If A has independent columns and we're at the point where Ax = 0.
* then x = 0, the only thing in the nullspace is 0
* Columns are definitely independent if they're perpendicular unit vectors (orthonormal vectors).
 |
| case of orthonormal 01 |
 |
| case of orthonormal 02 |
________________________________________________________________________________________________
MIT Gilbert Strang : Lecture 17 ( Orthogonal basis and Gram-Schmidt )
Orthogonal basis q1,---,qn
Orthogonal matrix Q
Gram-Schmidt A -> Q
** Q^T Q = I
If Q is square then Q^T Q = I tells us Q^T = Q^-1
* example with a permutation matrix
another example with unit vector
The length of the orthogonal matrix should be 1.
orthonormal 2-Dimensional space basis
3-D orthonormal
Suppose Q has orthonormal columns,
Project onto its column space
* P = Q(Q^T Q)^-1 Q^T = QQ^T { = I if Q is square }
* The benefit of Q^T Q x^ = Q^T b is that Q^T Q = identity matrix.
** So it's like x^ = Q^T b
so the i-th component is the i-th basis vector times b
** Gram-Schmidt
independent vectors a, b
orthogonal A, B -> orthonormal q1 = A/||A|| q2 = B/||B||
A can be orthonormal but b is not orthogonal to a, so we should make it orthogonal to A.
B is error and B = b - ((A^T * b) / (A^T * A)) * A
** A ⊥ B
* A^T(b - ((A^T * b) / (A^T * A)) * A) = A^T* b - A^T b = 0
In 3-dimensional space,
example
 |
| original matrix example |
matrix with orthonormal column
** A = LU A = QR
________________________________________________________________________________________________
MIT Gilbert Strang : Lecture 18 ( Properties of Determinants )
Determinants det A
Properties 1,2,3,4-10
± signs
** The real big reason for the determinants is the eigenvalues.
* det A = |A|
Properties of det
1) det I = 1
3) The determinant is a linear function of the first row if all the other rows stay the same.
** LINEAR EACH ROW SEPARATELY
4) 2 equal rows -> det = 0
exchange those rows -> the same matrix
5) Subtract L * row-i from row-k
DET doesn't change
6) Row of zeros -> det A = 0
7) det U = d1 * d2 * ---- * dn
product of the pivots
 |
| upper triangle |
8) * det A = 0 * when A is singular
* det A ≠ 0 when A is invertible,
a matrix is invertible when it produces a full set of pivots.
check
det is ad - bc
9) det AB = (detA) * (detB)
det A^-1 = 1/det A
A^-1 A = I (detA^-1) (detA) = 1
* detA^2 = (detA)^2
* det2A = 2^n * detA
10) det A^T = detA
prove # 10 |A^T| = |A|
|U^T L^T| = |LU| => |U^T| |L^T| = |L| |U|
________________________________________________________________________________________________
MIT Gilbert Strang : Lecture 19 ( Determinant Formulas and Cofactors )
Formula for detA (n! terms)
Cofactor formula
Tridiagonal matrices
By using separate linearity it can be divided into 4 easy determinants.
* a big formula for the determinant
det A = ∑±
n! terms
Example
( 4, 3, 2, 1 ) -> +1 ( 3, 2, 1, 4 )->-1





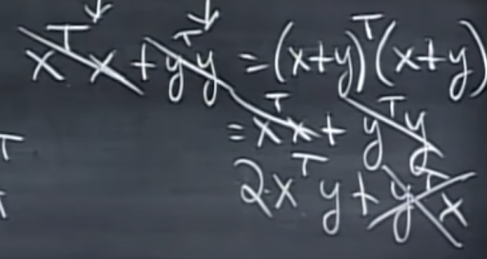
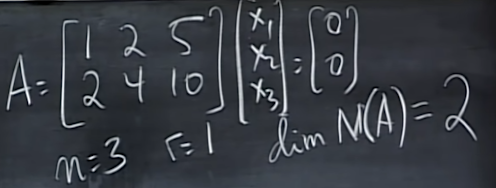
































































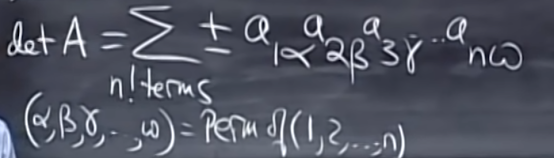

댓글
댓글 쓰기