Math simbols

Mathematical Symbols

TLatex can display dozens of special mathematical symbols. A few of them, such as + and > , are produced by typing the corresponding keyboard character. Others are obtained with the commands in the following table:

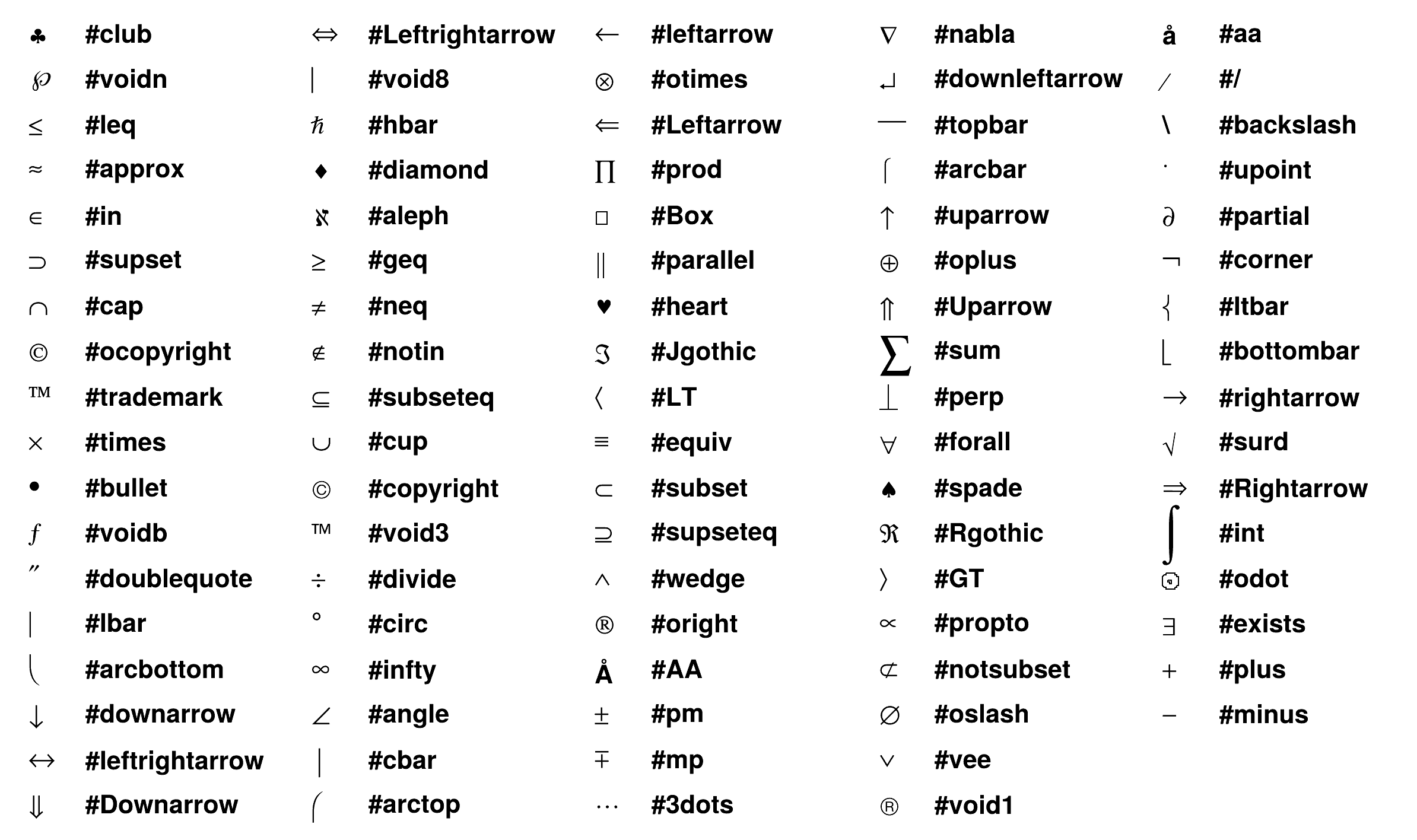
Delimiters

TLatex provides 4 kinds of proportional delimiters:

#[]{....} or "a la" Latex #left[.....#right] : big square brackets
#{}{....} or              #left{.....#right} : big curly brackets
#||{....} or              #left|.....#right| : big absolute value symbols
#(){....} or              #left(.....#right) : big parentheses

Greek Letters

The command to produce a lowercase Greek letter is obtained by adding a # to the name of the letter. For an uppercase Greek letter, just capitalize the first letter of the command name. Some letters have two representations. The name of the second one (the "variation") starts with "var". The following table gives the complete list:

he following example, in which all expressions are typeset in display math mode, contrasts the visual appeal of three separate integral expressions: the Gamma function, the Beta function (in a form that involves a fractional term), and an entirely fictitious integral expression that involves a double fraction term. Speaking for myself, I'd stay that only in the third case is it defensible to use \int\limits instead of just \int. Observe that the example code also demonstrates that issues of excessive amounts of white space between the integral symbol (and its side-set limits of integration) and the integrand are best dealt with by applying one or more \! (negative thinspace) instructions rather than by setting the limits of integration above and below the integral symbol.

enter image description here

\documentclass{article}
\usepackage{amsmath}
\begin{document}
\begin{align*}
\Gamma(z)=\int_0^\infty \!\! e^{-x}x^{z-1}\,dx 
  \quad&\text{vs.}\quad 
  \Gamma(z)=\int\limits_0^\infty e^{-x}x^{z-1}\,dx\\
B(x,y) = \int_0^\infty \!\! \frac{t^{x-1}}{(1+t)^{x+y}}\,dt
  \quad&\text{vs.}\quad
  B(x,y) = \int\limits _0^\infty \frac{t^{x-1}}{(1+t)^{x+y}}\,dt\\
\int_{-\infty}^\infty \frac{\frac{a(x)}{b(x)}}{\frac{c(x)}{f(x)}}\,dx 
  \quad&\text{vs.}\quad
  \int\limits_{-\infty}^\infty \frac{\frac{a(x)}{b(x)}}{\frac{c(x)}{f(x)}}\,dx
\end{align*}
\end{document}